Matrix Operations - Applications

Wondering why learn matrix and several operations performed on it. Lets see real world application of it !!!

The not so difficult - TRANSPOSE operation

Notice how the subscripts changed....Row number becomes column number and vice versa.

You can apply this concept to tansform an image through java programming.
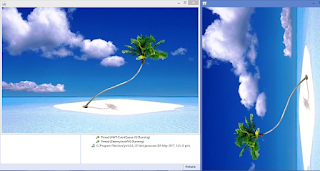
Original Image - Small-Island.jpg

package image_processing;

import java.awt.Color;

import java.awt.image.BufferedImage;

import java.io.File;

import java.io.IOException;

import javax.imageio.ImageIO;

import javax.swing.ImageIcon;

import javax.swing.JFrame;

import javax.swing.JLabel;

public class Transpose{

    public static void main(String[] args) throws IOException {

        JFrame frame1 = new JFrame();

        BufferedImage image = ImageIO.read(new File("Small-Island.jpg"));

        ImageIcon icon = new ImageIcon(image);

        JLabel label1 = new JLabel();

        int width = image.getWidth();

        int height = image.getHeight();

        label1.setIcon(icon);

        frame1.add(label1);

        frame1.setSize(width, height);

        frame1.setVisible(true);

        frame1.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

        BufferedImage image2 = new BufferedImage(height, width, BufferedImage.TYPE_3BYTE_BGR);

        for(int y=0; y<height; y++){

            for(int x=0; x<width; x++){

                // get colour at point(x,y)

                Color c = new Color(image.getRGB(x, y));

                // transpose

                image2.setRGB(y, x, c.getRGB());

            }

        }

        File ouptut = new File("transpose.jpg");

        ImageIO.write(image2, "jpg", ouptut);

        ImageIcon icon2 = new ImageIcon(image2);

        JFrame frame2 = new JFrame();

        JLabel label2 = new JLabel();

        label2.setIcon(icon2);

        frame2.add(label2);

        frame2.setSize(height, width);

        frame2.setLocation(width,0);

        frame2.setVisible(true);

        frame2.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

    }

}

After you execute this program you get - transpose.jpg

Output of the program :

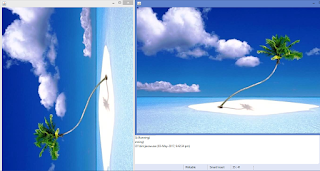
And when we say that (Aꞌ)ꞌ=A i.e., transpose of a transposed matrix is the matrix itself we mean this:

To get this output from the above program just make 2 simple changes: 1. Replace filename Small-Island.jpg with  transpose.jpg  and filename transpose.jpg  with original.jpg       


After learning from this example you can think of transforming your images in multiple ways. Just imagine your image as a matrix of colored pixels and play around by manipulating these with matrix operations like addition, subtraction, multiplying with a scalar value and observe the effects.




Matrix Multiplication


Lets see this through a real life problem.
I am a medicine whole seller. 2 retailers Ravi and Dheeraj come to me to purchase Nise and Stamlo tablets. Ravi orders 100 strips of Nise, 50 strips of Stamlo. Dheeraj orders 200 strips of Nise and 20 strips of Stamlo.
1 strip of Nise costs Rs. 62 while 1 strip of Stamlo costs Rs. 49
How much does each retailer pay?

We can solve this problem with the help of matrix multiplication.

A simple java program that does this calculation:

import java.util.Arrays;

public class MatrixMulti {

    public static void main(String[] args){

        int qtyMatrix[][] = {

                {100, 50},

                {200,20}

        };

        int priceVector[] = {62, 49};

        int costVector[] = new int[2];

        for(int row=0; row<2; row++){

            costVector[row] = 0;

            for(int col=0; col<2; col++){

                costVector[row] += qtyMatrix[row][col] * priceVector[col];

            }

        }

        System.out.println(Arrays.toString(costVector));

    }

}

Output : [8650, 13380]

So Ravi pays Rs. 8650 and Dheeraj pays Rs. 13380.

This program can be scaled more to get dimensions from user as input to solve a problem of much larger magnitude where there can be 'n' number of retailers and 'm' kinds of medicines. Here the focus was on making the concept clear by using a simple application.




Inverse Of A Matrix

Extending the above example, suppose after a few months I look at old data, and I only have the transactional data i.e, the quantities that were purchased by Ravi and Dheeraj and the total price paid by them. How do I find out what was the price of each strip of Nise and Stamlo at that point of time as now the price might have changed!

Lets arrange the data in the same way again:

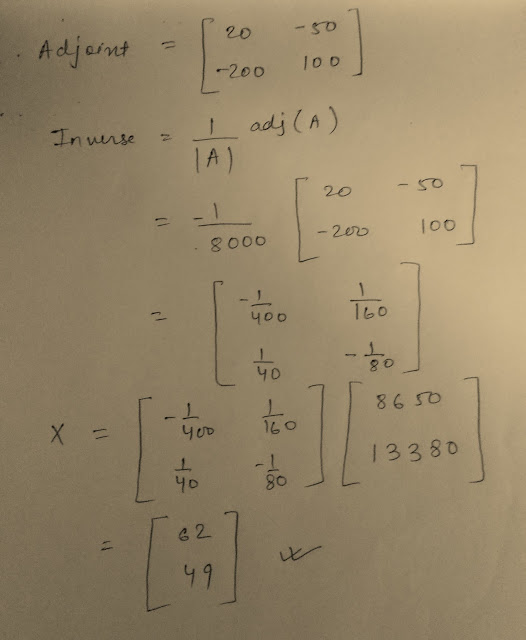
This time in order to find the price vector X we just multiply the cost vector with inverse of quantity matrix and we get the price per strip of the medicines i.e., Rs. 62 and Rs. 49

Writing a program for this in java to solve this problem is very lengthy process, whereas programming of matrices is deeply built into R Language. What we want to achieve above is just a matter of 2 commands in R, i.e,

A %*% B	Matrix multiplication
solve(A)	Inverse of A where A is a square matrix.

Of course we need to define the quantity matrix and the cost vector first as follows:

A = matrix(data = c(100, 50, 200, 20), nrow = 2, ncol = 2,byrow = TRUE)
B = matrix(data = c(8650, 13380), nrow = 2, ncol = 1, byrow = TRUE)

Next the 1 step solution :

X = solve(A) %*% B

A look at the R console:

We get the medicine price in vector X.